Vector Movement In Space Games
A Critical Look At Three Systems
The Editor
There are several games about combat between spaceships out there.
Perhaps surprisingly, none have been wildly successful, but a great
variety exists nonetheless. Speaking in broad terms, these games
and their players can be divided in two categories: Those just looking
for a little fun blowing up the
Death
Star and those looking for
realism.
 For a number of reasons, realism isn't such a hot item in
Hollywood portrayals of space
combat (or their portrayal of pretty much anything
else), which leads
to the popular
image of space combat being something like
WWII battleships in
space.
Consequently, most of the rulesets out there try to capture the
silver screen feel.
For a number of reasons, realism isn't such a hot item in
Hollywood portrayals of space
combat (or their portrayal of pretty much anything
else), which leads
to the popular
image of space combat being something like
WWII battleships in
space.
Consequently, most of the rulesets out there try to capture the
silver screen feel.
But a vocal subgroup of space miniatures gamers is looking for more
realism, and realism in this context usually means more realistic
movement system (these same people typically accept lasers, particle
beams and FTL at face
value).
One manifestation of this quest for realism is the 3-D movement
system, in various incarnations. Sort of obvious, but actually of
less use than in traditional air warfare games. But we'll ignore that
for now and concentrate on the other big thing in space combat realism.
Namely, vector movement. The attempt to apply
Newtonian
physics to space games (as if they somehow did not apply to
movement anywhere else). Vector movement, ah, the ultimate in realism,
elevating space games to a completely new level, a veritable
nirvana of
frictionless gaming...
Except that I'm not too thrilled about it.
Why?
Because I didn't sleep through
High School Physics.
Elementary Physics
 What we're talking about is
Newton's
three laws of motion. As the point I'm about to make is about
High School Physics, I'm ignoring a lot of stuff here to present a very
simplistic model.
What we're talking about is
Newton's
three laws of motion. As the point I'm about to make is about
High School Physics, I'm ignoring a lot of stuff here to present a very
simplistic model.
The first law states that an object in motion continues in motion
unless force is applied. As there is virtually no drag (read:
external force slowing movement) in space, in practical
gaming terms this means that speed builds up.
The second law states that force equals mass times acceleration. The
important bit here is that force maintains acceleration, not velocity
- a radical departure from classical Greek thinking, but in practical
gaming terms it means the same thing as the first law.
The third law is actually the one that makes rocket engines and
therefore space travel as we currently know it possible. Consequently,
it is ignored by pretty much all game systems. So shall we, for the
time being.
Does this directly relate to gaming? Not really. What we are really interested
in are two basic formulas of
kinematics.
Velocity under constant acceleration: current velocity equals initial velocity
plus acceleration times the time spent accelerating. Or
v = v0 + a * t
Simple enough. However, enter the realm of higher mathematics with
this one:
Distance traveled under constant acceleration equals initial velocity
times time traveled plus one half acceleration times time squared. Or
d = v0 * t + 0.5 * a * t^2
That's it. Simple really, isn't it? Let's see how certain game
systems handle this.
In This Corner...
 The space combat system of the ill-fated Renegade Legion line originally
published by FASA,
then by Crunchy Frog, then
FASA again and now probably no one... but the nice armor system
was resurrected in
Crimson
Skies, except the original boardgame version of that is out
of print too...
The space combat system of the ill-fated Renegade Legion line originally
published by FASA,
then by Crunchy Frog, then
FASA again and now probably no one... but the nice armor system
was resurrected in
Crimson
Skies, except the original boardgame version of that is out
of print too...
As typical, the vanilla movement system is pure Hollywood, but
optional rules exist for vector movement. The game is played on
a hex map, which makes turning somewhat granular.
 Originally known as ΔV, published in 2003 by Ad Astra Games. It is designed
from ground up to be a vector game unlike most of the competition.
However, Attack Vector also uses hexes, which introduces a
certain amount of granularity.
Originally known as ΔV, published in 2003 by Ad Astra Games. It is designed
from ground up to be a vector game unlike most of the competition.
However, Attack Vector also uses hexes, which introduces a
certain amount of granularity.
The results here are based on a pre-publication version of ΔV,
which the publisher was kind enough to send me.
When Full Thrust was originally published by
Ground Zero Games,
it was firmly in the
Hollywood realm, and quite rightly so. But after demands from fans
and a couple of
unofficial
variant systems
on the web, an optional vector movement system was published in
Fleet Book 1.
As a pure tabletop game, Full Thrust does not suffer from
granularity quite to the same degree as hex-based systems.
The Tests
 We'll take three simple test cases and see how each of these rules
handles it, and what results you would get if you applied your
knowledge of High School Physics to the same problem.
We'll take three simple test cases and see how each of these rules
handles it, and what results you would get if you applied your
knowledge of High School Physics to the same problem.
The basic unit of time is one game turn. This makes the
calculations even easier without really compromising anything
- we are talking in somewhat abstract terms here anyway.
All test results are based on the rules as printed. Errata,
FAQs, Internet discussions etc. that do not come with the rulebook
when picked up from a random game store shelf are not considered.
A note to algebra purists: The following calculations are presented
in a slightly informal way with many of the variables replaced by
specific numbers. This is done to make this easier to understand
for
general
audiences, not to imply that the cases aren't general
in nature.
Test 1: Acceleration
Let's start with a simple one-dimensional case. Yes, you heard me right,
1-D. Just constant acceleration of one unit for a couple of
turns. We are interested in three things:
- velocity at the end of each turn
- distance traveled during the turn
- total distance traveled
Constant acceleration in straight line
| Game Turn | Variable |
Game System |
| Interceptor | Attack Vector | Full Thrust |
High School Physics |
| 1 | velocity | 1 | 1 |
1 | 1 |
| distance | 1 | 1 |
1 | 0.5 |
| total distance | 1 | 1 |
1 | 0.5 |
| 2 | velocity | 2 | 2 |
2 | 2 |
| distance | 2 | 3 |
2 | 1.5 |
| total distance | 3 | 4 |
3 | 2 |
| 3 | velocity | 3 | 3 |
3 | 3 |
| distance | 3 | 5 |
3 | 2.5 |
| total distance | 6 | 9 |
6 | 4.5 |
| 4 | velocity | 4 | 4 |
4 | 4 |
| distance | 4 | 7 |
4 | 3.5 |
| total distance | 10 | 16 |
10 | 8 |
Note: Attack Vector numbers halved for this chart.
See below for an explanation.
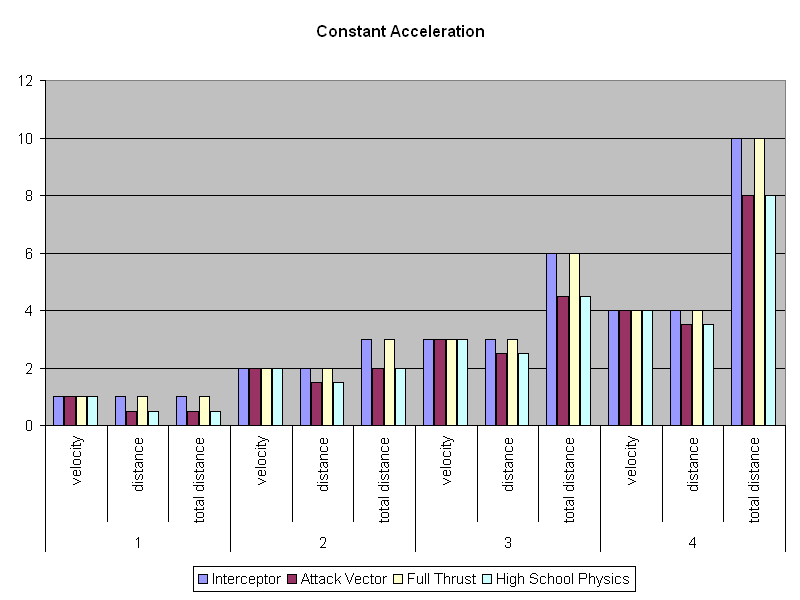
Results
As you can see, all systems model current velocity just fine. However,
looking at distance traveled during each game turn and the total distance
traveled, we are beginning to see differences.
The Attack Vector numbers look a bit funny until you realize each hex
is actually half a unit, a necessary tweak to show half-unit
movement on a discrete hexmap. Then it all clicks into place and
the numbers are actually exactly correct. Attack Vector numbers are
halved in the chart for comparison purposes.
But in case of Full Thrust and Interceptor,
the problem is systematic and
cumulating.
In fact, Full Thrust and Interceptor are not modeling constant
acceleration at all, but something
completely
different.
The full effect of the acceleration is applied at the start of
each turn, instead of gradually over the time period.
Test 2: Stopping
 The previous test might seem like small potatoes, but consider this
example:
The previous test might seem like small potatoes, but consider this
example:
You are cruising along peacefully, when suddenly a
giant foot descends from
heaven and blocks your path.
Conveniently, you are travelling at velocity that equals your one
turn's acceleration, which just happens to be one (two in case
of Attack Vector).
The foot is directly in front of you (distance zero).
Assume that switching the thrusters to braking takes
effectively no time.
Interpreting the previous results slightly differently, we get
the following results:
Emergency brake
| Game System |
| Interceptor | Attack Vector | Full Thrust |
High School Physics |
| Final velocity | 0 | 0 |
0 | 0 |
| Collision with foot | No | Yes |
No | Yes |
Results
How convenient for Full Thrust and Interceptor players!
If the designers of these games would only sell this technology
to car manufacturers,
they'd be millionaires!
Attack Vector pilots must actually invest in some seat belts and
airbags, as their game manages
to replicate High School Physics in this respect.
Test 3: Turning
 Many people think that the important thing about vector movement is
that your guns don't have to point the way you're going. But any
old tank
can do that.
Many people think that the important thing about vector movement is
that your guns don't have to point the way you're going. But any
old tank
can do that.
No, the really important bit is that your traction is zero. This
becomes especially important when you want to change the direction
you're going, i.e. actually turning your course instead of just
pointing your nose.
Mathematically, it would be easiest to calculate a 90-degree turn
because the vectors would be
orthogonal.
However, hex-based systems handle everything in increments of 60
degrees (one hexside), so we're going to choose a test which gives our
hexbound contestants a sporting chance.
Twist and Shout
Or rather
turn
and burn. We'll assume that the ship is coasting at speed equal
to four turns' acceleration, with nose pointed 120 degrees to right.
At the start of the test, the ship begins to apply thrust in the
direction its nose is pointing, and continues this for some time.
The following picture shows the position of the ship at the end of
each turn.
Again, we'll halve the Attack Vector numbers to scale it to match the others.
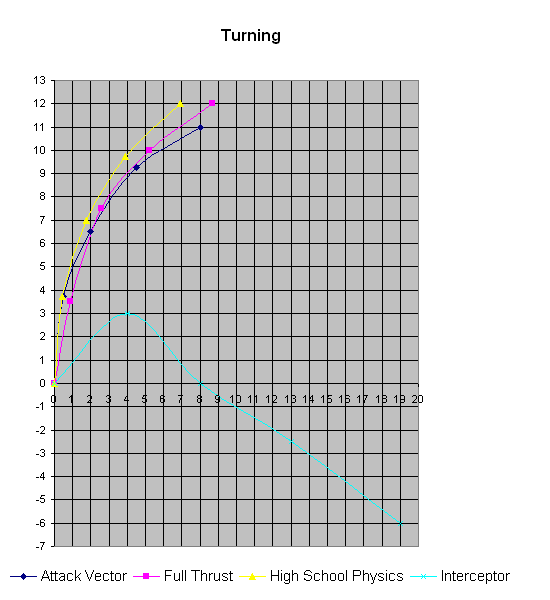
Results
Well, Interceptor is clearly in a class of its own. This isn't really
vector movement at all, it's basically Hollywood movement with
spinning-while-coasting added.
Which, incidentally, is pretty much what
Babylon 5 space combat actually
looks like.
Another interesting thing is what happens to Attack Vector. After
spending many painful moments plotting drifts and calculating
vector changes, the hex grid granularity actually pries the Attack
Vector apart from the real one.
Full Thrust actually handles pretty well. The velocity vector is
correct, but the faulty displacement handling makes the turn
tighter than it should be.
 Finally, it should be noted that all of the tested rules exaggerate
the turning ability. Pure coincidence or cutting corners to improve
playability?
Finally, it should be noted that all of the tested rules exaggerate
the turning ability. Pure coincidence or cutting corners to improve
playability?
It would be easy to extend these calculations for Full Thrust and
High School Physics. In fact I've done so. Unfortunately, for
Attack Vector it would mean a boatload of tedious counting of hexes...
The extended numbers can
be downloaded as an
Excel sheet.
Test 4: Turning and Acceleration
"Hey, you said three tests! Not fair!", I hear you say. Well, yes.
Let me explain why there is no fourth test.
The logical progression here would to be to apply thrust and turning
the same time. But solving these cases would require
differential
equations, which I believe is slightly out of the realm of
High School Physics. It'll be the first thing they'll hit you with when
you go to a real school, though...
Like the fourth
child, that's it for this one's airtime.
To give credit where credit's due, Attack Vector can handle a fair
approximation of this.
In The Good Old Days
 If you are old enough, you might remember classic video games such
as
Asteroids
and
Lunar Lander. I loved
these games. The thing that made them fun was that they were based
on a simple Newtonian movement model. Incidentally, these games used
vector graphics, but that's
not really related to our issue here. Goes to show all
vectors
are not created
equal, though.
If you are old enough, you might remember classic video games such
as
Asteroids
and
Lunar Lander. I loved
these games. The thing that made them fun was that they were based
on a simple Newtonian movement model. Incidentally, these games used
vector graphics, but that's
not really related to our issue here. Goes to show all
vectors
are not created
equal, though.
When I'm thinking of even
semi-realistic
space movement, I'm thinking of these games. They demonstrate the basic
principles so clearly and intuitively.
Lunar Lander
In Lunar Lander, your job is to apply thrust gently to ease the lunar
module down without making a new crater in the pock-marked lunar
surface.
Sounds simple, doesn't it? Ok, there's a time limit in form of limited
fuel, but still... Then why is your lunar module going up instead of
down?
Because you overcompensate. You apply thrust until you see the module
slowing down to a crawl. But the problem is that your perception of
speed is based on the distance you saw the module travel on screen. As
we saw earlier, the distance traveled under constant acceleration
does not match the change in velocity. In fact, it's exactly half.
So, when you apply enough thrust to cancel out the accumulated downward
velocity, you are actually turning the velocity vector 180 degrees, to
straight up! The gravity is actually the only thing that saves your bacon
from being flung to outer space.
That's what makes Lunar Lander hard. That's what makes it interesting.
And that's what the lesser vector system utterly fail to handle.
Asteroids
Spin to correct heading, apply correct thrust, repeat. Sounds simple
enough.
 While not
Pac-Man,
Asteroids was a raving success. And no small wonder, the game is a
blast.
While not
Pac-Man,
Asteroids was a raving success. And no small wonder, the game is a
blast.
Why is it fun, even more fun than Lunar Lander? Because you never have
enough time to do things neatly. The ship turns so painfully slowly
when an asteroid is zooming in on you... you end up hitting the thrusters
even though you're not quite heading in the right direction... or worse yet,
hitting thrusters and trying to turn at same time - a tactic that
almost inevitably ends in the spiral of doom.
There is a very good game design reason the
teleport
button kills your inertia too...
Asteroids shows you in very clear terms how hard it is to
change your course in space and what sheer madness turning
and thrusting at the same time results in.
Inevitably, when I'm considering a space game, I remember these two
classics. If the game claims realism, these are the benchmarks I
measure it against.
And, for the most part, they fail to do even what a simple computer
game from early eighties did, nevermind even skimming the
more advanced stuff.
Conclusion
The results are pretty clear. Attack Vector is the only game
of the three presented here that has any claim to presenting
realistic space movement.
Does that mean I like it? Not really. It is far too complex for my
current tastes. I gave up phased movement with
Car Fleet Battles.
However, when something is touted as realistic and I can poke
holes in using only my vague recollection of High School Physics,
I feel my intelligence has been insulted. These systems are not
realistic, so the question turns to are they fun. In my humble
opinion, they do not bring anything to the
games besides additional complexity.
If you really want realism, go with something like Attack Vector.
If you just want to play, use the Hollywood movement systems.
Q.E.D.
P.S. Incidentally, the new Car Wars is much simpler than what I
used to play.
P.P.S. Besides, in full realism you can't do
sound effects,
where's the fun in that?
Comments
| Attack Vector dating |
maxxon |
Oct 23, 2003 10:37 |
In all honesty, I should mention that my pre-publication copy of deltaVee(Attack Vector) is dated July 18th, 2000.
Ken Burnside from Ad Astra tells me the game has evolved much since (unlike the other contestants). I believe that if this article makes Attack Vector sound like a game you'd like to play, the new edition will deliver more of it.
|
| Attack Vector dating and evolution. |
burnside |
Oct 23, 2003 21:10 |
I'm actually amazed, having looked at the old file from July 18 2000, that Mikko was able to follow enough of the game to get as favorable an impression as he did.
It has been mucn streamlined, and now works in 3-D....including 12 point facing on a hex map (which will still have the hex grain error Mikko compained of). We do show the integral of fuel mass over dry mass of the ship when calculating total delta V; running at nearly empty tanks doesn't increase your max thrust rating because the fuel fractions we use result in changes below the granularity of the game. You do get some "extra" fuel dots for having nearly empty tanks, though.
We now have physically correct pivots and rotations, handled in clean charts that are pretty easy to use. We know how much energy goes into a damage point, and what the armors are made of. We know the aperture size and wavelength of our lasers in the game, and all sorts of crunchy engineering details that, well, are there in sidebars to show how the rules came to be, but which the player doesn't need to know to play it.
Every physics problem someone has given us, we've solved and put into mechanics in the game. There are a few engineering implausibilities...but very few people will be offended that we have engines capable of pushing 5,000 ton frigates around in whopping quarter g increments without melting.
While we have phased movement, we have only 8 phases per turn, and the decision making is all simultaneous. I've seen 3-D 7-on-7 squadron/fleet actions running at 10-20 minutes per turn, with upwards of 1000 individually tracked missiles in flight...all because we tossed I-Go/U-Go in favor of "OK, everyone place future position marker. OK, everyone, check off your order boxes. OK, reveal fire. (resolve fire) OK, reveal long orders. (turn on engines, begin pivots, set persistent rotations...) OK, resolve thrust, move to future position marker. Anyone need to re-do their movement grid? No? OK, regenerate power. Segment 2. Place future position marker..." It literally takes about as long to play out a segment as it does to read that paragraph out loud twice.
We try to minimize special cases. We try to make everything flow logically from the rules.
I actually prefer board games to computer games for this kind of simulation. A boardgame will give you a better understanding of what's going on. There's a bit of time to think...and compared to asteroids, there's a bit less granularity.
One thing that makes AV:T somewhat different is that you shouldn't even TRY to do precise maneuvers. This results in iterative hex counting and sucks the fun out of the game. Instead, decide roughly what vectors you want by the end of the turn, and keep it as a guideline for the maneuvers you want to perform. As people do other things the maneuvers you make won't match that guideline...but in the end you fly by the seat of your pants.
To see the complete Sequence of Play and other play aids, go to
http://www.adastragames.com/downloads.html |
| Weee |
Paul Brown (guest) |
May 01, 2013 08:52 |
Thanks for this article dude. Found it very informative from a science-based perspective.
Though I wouldn't mind if one day you took it to round 4 and did the double equation thing :) |
| The fourth test |
maxxon |
May 02, 2013 08:30 |
I'm glad you liked it.
The first thing with the fourth test is that only Attack Vector models it at all and then only because it has phased movement. Then you could argue that an Attack
Vector phase is actually equal to a turn in other games and the comparison starts to get messy.
Assuming starting from standstill (an odd concept in a space game, but let's go with it for now) with realistic physics you would see the ship spinning in a fairly tight but slowly widening circle. A bit like a car doing donuts. Due to the discrete handling in games, the ship will be to travel a fair bit farther
before any canceling thrust can be applied, thus creating a rapidly expanding spiral. Many won't be able to make a full circle before falling off the table (the edge of space, another interesting concept, perhaps for another article).
And the other thing is that I haven't actually needed or used differential equations for anything in the past couple of decades, so I'm a tad rusty with actually solving them.
And, as I said, differential equations are beyond high school physics, I think. |

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 2.5 License.
Copyright 2003-2021 Mikko Kurki-Suonio
 For a number of reasons, realism isn't such a hot item in
Hollywood portrayals of space
combat (or their portrayal of pretty much anything
else), which leads
to the popular
image of space combat being something like
WWII battleships in
space.
Consequently, most of the rulesets out there try to capture the
silver screen feel.
For a number of reasons, realism isn't such a hot item in
Hollywood portrayals of space
combat (or their portrayal of pretty much anything
else), which leads
to the popular
image of space combat being something like
WWII battleships in
space.
Consequently, most of the rulesets out there try to capture the
silver screen feel.
 What we're talking about is
What we're talking about is
 The space combat system of the ill-fated Renegade Legion line originally
published by
The space combat system of the ill-fated Renegade Legion line originally
published by  Originally known as ΔV, published in 2003 by Ad Astra Games. It is designed
from ground up to be a vector game unlike most of the competition.
However, Attack Vector also uses hexes, which introduces a
certain amount of granularity.
Originally known as ΔV, published in 2003 by Ad Astra Games. It is designed
from ground up to be a vector game unlike most of the competition.
However, Attack Vector also uses hexes, which introduces a
certain amount of granularity.
 We'll take three simple test cases and see how each of these rules
handles it, and what results you would get if you applied your
knowledge of High School Physics to the same problem.
We'll take three simple test cases and see how each of these rules
handles it, and what results you would get if you applied your
knowledge of High School Physics to the same problem.

 The previous test might seem like small potatoes, but consider this
example:
The previous test might seem like small potatoes, but consider this
example:
 Many people think that the important thing about vector movement is
that your guns don't have to point the way you're going. But any
old
Many people think that the important thing about vector movement is
that your guns don't have to point the way you're going. But any
old 
 If you are old enough, you might remember classic video games such
as
If you are old enough, you might remember classic video games such
as
 While not
While not
 Sucks!
Sucks!
